AI Answer Evaluation Platform Live Now. Try Free Answer Evaluation Now
Hardy Weinberg Equilibrium
Hardy Weinberg Equilibrium is concerned with the distribution of frequency of genotypes of alleles in a population. The underlying premise of this Equilibrium is that, in a large population with random mating and lack of additional factors like genetic drift, mutation, and natural selection the frequencies of certain genes tends to remain constant from one generation to another.
Hardy Weinberg equilibrium maintains a very idealised and hypothetical condition, it can aid in identifying the genetic variations brought on by mutation, migration, genetic drift, non-random mating, and natural selection throughout the course of generations.
Background and Historical Context
The Hardy Weinberg Equilibrium, which deals with the frequency of alleles in a population, was developed in 1908 by German Physician Wilhelm Weinberg and English mathematician G. M. Hardy.
The importance of the Hardy Weinberg Equilibrium in population genetics is that it may be used to compare observed allele frequencies to mathematically estimated allele frequencies to determine whether or not evolution has occurred. Also, the Hardy Weinberg equilibrium offers population geneticists a benchmark to measure real conditions against the standard conditions.

Understanding the Hardy Weinberg Equilibrium
There are certain conditions where the genotype and allele frequency remains constant from one generation to another.
The conditions are as follows:
- Large population size
- Sexual reproduction
- Allele frequency between male and female should not differ
- Diploid organisms
- No overlap of generations
- Random mating
- No mutation
- No gene flow i.e., migration
- No natural selection
Hardy Weinberg Equilibrium:
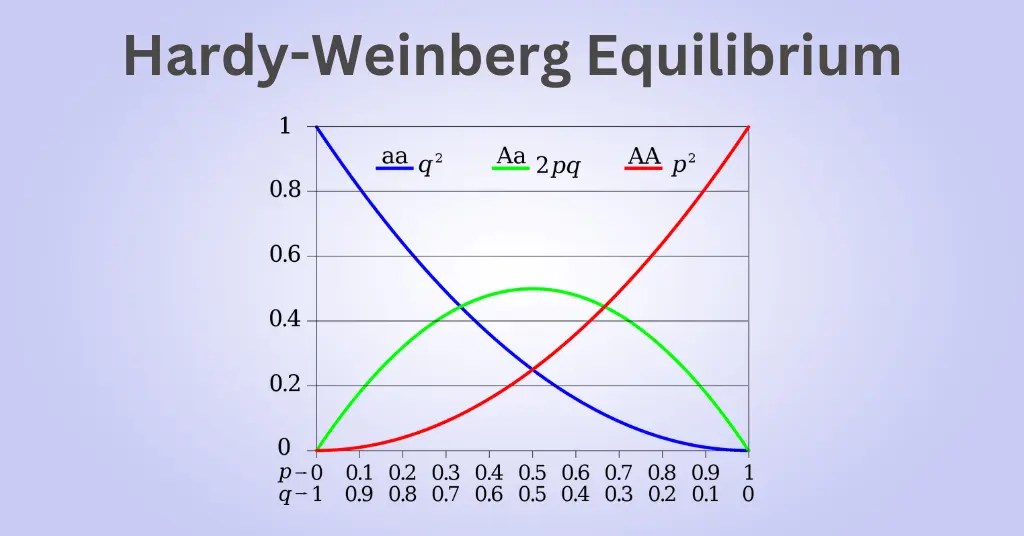
The Hardy Weinberg equation is expressed as (p+q) = 1 OR (p+q)2 = 1 that can also be written as p2+2pq+q2
Where,
p = frequency of a dominant allele in a population
q = frequency of a recessive allele in a population
p2 = frequency of homozygous dominant individuals (%)
q2 = frequency of homozygous recessive individuals (%)
2pq = frequency of heterozygous individuals
Example: To further comprehend this consider an example of Phenylthiocarbamide (PTC) tasting which is an autosomal dominant trait. The people that are tasters are determined by the allele T and with genotype TT and Tt and it is considered as a dominant character whereas the non-tasters are determined by allele t and with genotype tt that is considered to be a recessive character. Consider a population of 1000 individuals, of whom 400 individuals are homozygous dominant tasters, 400 are heterozygous tasters and 200 are homozygous recessive non-tasters.
In a population of 1000 individuals the total number of alleles present is 2000.
p = 800+400 ÷ 2000 (800 alleles obtained from homozygous dominant and 400 from heterozygous)
p = 0.6
q = 400+400 ÷ 2000 (400 alleles obtained from homozygous recessive and 400 from heterozygous) OR simply p = (1 – 0.6)
q = 0.4
p2 = (0.6)2 = 0.36
q2 = (0.4)2 = 0.16
2pq = 2 (0.60.4) = 0.48
According to Hardy Weinberg equation;
(p+q)2 = p2 + 2pq + q2
= 0.36 + 2 (0.60.4) + 0.16
= 1
Hence the frequency of TT = 0.36%, Tt = 0.48%, tt = 0.16%
If the values of p and q remain constant from generation to generation where the dominant and the recessive phenotypes will stay in the same ratio across all the generations then it is considered that the population is in Hardy Weinberg equilibrium.
Factors that Affect the Hardy Weinberg Equilibrium
There are mainly five factors that can cause disruptions from the Hardy Weinberg equilibrium;
- Mutation – Mutation is the basis of evolution. Because mutational events are often quite rare and low and the allele frequency cannot be swiftly modified by a single mutation, mutation rate is crucial. Repeated mutations in a population causes deviations in genetic equilibrium. The role mutation plays can clearly be understood with an example – If there are 10 individuals in a population that contain ‘A’ and ‘a’ alleles then the population will have 3 kinds of genotypes AA, Aa, aa with the ratio 5:2:3 respectively. This population will contain 60% ‘A’ gene and 40% ‘a’ gene. Now in this same population if 1 dominant ‘A’ gene mutates to recessive ‘a’ gene then the ratio will be 4:3:3 where the population will contain 55% ‘A’ gene and 45% ‘a’ gene.
- Natural selection – Natural selection is the process whereby more adaptive individuals are chosen over less adaptive ones in a given population. Variations in population are brought about by several processes of evolution, and these differences can sometimes be advantageous and sometimes disadvantageous. The adaptable genotype is passed on to its progeny.
- Genetic drift – Genetic drift is the term used to describe the random shift in allele frequencies in a small population. Due to the tiny population size, some allele frequencies may rise, fall, or even disappear, changing the gene pool and eventually reducing genetic diversity. The founder effect, in which a small group establishes a population at a different place from their parent population, can cause genetic drift. The bottleneck effect, in which the population experiences a dramatic drop as a result of environmental factors, and can result in genetic drift.
- Migration (Gene flow) – The movement of alleles between populations is known as migration. Genetic variation is caused due to migration which eventually leads to genetic diversity in a population.
- Non-random mating – Random mating in itself does not occur which leads to the disruption of the Hardy Weinberg equilibrium. Non-random mating is a selective process.
Table 1: Evolutionary forces disrupting genetic equilibrium
| Evolutionary Force | Description | Effect |
|---|---|---|
| Small population size | Random fluctuations in allele frequencies | Alters genotype frequencies |
| Non-random mating | Increases homozygous individuals | Alters genotype frequencies |
| Mutation | Introduces new alleles | Changes allele frequencies |
| Migration (gene flow) | Movement of individuals in or out of a population | Alters allele frequencies |
| Selection (natural or artificial) | Increase in frequency of survival advantageous traits | Changes allele frequencies |
Conclusion
The Hardy Weinberg Equilibrium appropriately helps in assessing whether allele frequencies are indeed changing; if the allele frequencies and genotype do not change it can be stated that the population is in Hardy Weinberg equilibrium and if it does change, it can be concluded that the evolutionary forces are acting on the population.
By either raising or reducing the allele frequency, the evolutionary forces of mutation, natural selection, genetic drift, migration, and non-random mating can lead to departures from Hardy Weinberg equilibrium.
References
Mielke, J. H., Konigsberg, L. W., & Relethford, J. H. (2010). Human Biological Variation, 2nd Edition (2 edition). New York: Oxford University Press. pp. 47.
Jurmain, R., Kilgore, L., Trevathan, W., Ciochon, R. L., &Bartelink, E. (2017). Introduction to Physical Anthropology (15 edition). Boston: Wadsworth Publishing. pp. 425.




